Infinity is a concept that is hard to grasp. But it is also fun in sort of that brain teaser kind of way. Is it a number? Is one infinity greater than another infinity?
Steven Strogatz tells a story in his book the Joy of X about responding to a letter from a mom on behalf of her 6 years old son asking if infinity is odd or even. He responded by saying that if infinity were odd then two times infinity would be even, which is not possible since they are both infinity. The mom said her son was happy with that explanations since it kind of meant infinity was big enough to be both odd and even, which was not Strogatz's intent.
It is important to remember that infinity is not an actual number. To me personally, I consider a number to be something that is finite. Something you can represent with numerical notation. 1.7498 is a number to me, just as much as 7/189 and 5 are numbers. Infinity doesn't play by the same rules as numbers do. For example it is neither even nor odd. If infinity were a number by my definition, we would be able to count to it, or at least order it, which we obviously can not. Cantor, looked at infinity through the eyes of set theory. He defined cardinality as how many elements were in a set, and he viewed infinity as a measurement of how many elements were in certain sets. If we have the infinite set of all integers and then the infinite set of integers that are divisible by 100, which set will be larger? There is a much larger part of my mind that wants to say the set of all integers will be 99 times bigger obviously! But infinity is not a number, we can't compare it that way. They are both infinity. Neither set is larger than the other. The set of all integers contains numbers that are closer together on the number line than the set which are divisible by 100, but we can steadily add numbers to each set at the same rate for an infinite amount of time. We can have corresponding items in each set such as, 1 corresponds to 100, 2 corresponds to 200, and so forth. I'm not trying to tell you, if we counted each number in each set they would have the same amount of elements in each set. That is not the point, first of all we can't count to infinity. Therefore we can't compare infinities, and therefore both sets are infinitely large. They just happen to be different infinities. I like to think of infinity as a sort of all or nothing concept. Something is either infinite or it is finite. Two different infinite sets are both infinite, they are both the 'all' they just happen to be different 'alls'.
Wednesday, June 25, 2014
Weekly 6: History of Math: Women in Math
According to statistics found on nsf.gov there are 10,379,172 women in undergraduate programs across the United States compared to 7,933,477 men who are enroll in undergraduate programs across the United States. Despite the much greater number of women going to college, less than a quarter of the students in undergrad engineering programs are women. Also, only about 28% of Doctoral Degree in Math and Statistics were awarded to females. There must be a reason for this. Women just aren't as mathematically inclined. FALSE!
Some of the greatest mathematicians have been women, but they just haven't gotten the same amount of attention as their male counterparts. They also faced many more challenges when it came to getting a formal education and getting work published and recognized.
One amazing female mathematician was Emmy Noether. She was a German born mathematician, who was the daughter of a Mathematics professor. Maybe the math was just in her blood, but clearly math doesn't discriminate between men and women. She received a Ph.D. in mathematics in 1907, but worked for free and without a specific title at the Mathematics Institute Erlangen for 8 years. In 1915 she proved that any differentiable symmetry of the action of a physical system has a corresponding conservation law. This later came to be known as the Noether's Theorem. She later worked under Hilbert at Gottingen University. She was only allowed to work under Hilbert as his assistant because she was a women. It wasn't until Hilbert and Einstein (yes that Einstein) stood up for her, was she allowed to lecture on her own, but she still wasn't paid for her work. She left Europe and came to the United States in 1933, because of the rise of the Nazi regime and her Jewish background. Her body of work led to developments in geometry, algebra, and topology.
Math doesn't hold any prejudices or biasses, people are the ones who hold each other back. The subject of mathematics is open for discovery. While some genders have the stereotype of being stronger in some subjects, those stereotypes should not hold people back from doing what they excel at. Those such as Noether who went against stereotypes and continued working on what they loved, proved that the subject of math is ready for whatever you want to do with it, no matter the reaction it may evoke from others.
Some of the greatest mathematicians have been women, but they just haven't gotten the same amount of attention as their male counterparts. They also faced many more challenges when it came to getting a formal education and getting work published and recognized.
One amazing female mathematician was Emmy Noether. She was a German born mathematician, who was the daughter of a Mathematics professor. Maybe the math was just in her blood, but clearly math doesn't discriminate between men and women. She received a Ph.D. in mathematics in 1907, but worked for free and without a specific title at the Mathematics Institute Erlangen for 8 years. In 1915 she proved that any differentiable symmetry of the action of a physical system has a corresponding conservation law. This later came to be known as the Noether's Theorem. She later worked under Hilbert at Gottingen University. She was only allowed to work under Hilbert as his assistant because she was a women. It wasn't until Hilbert and Einstein (yes that Einstein) stood up for her, was she allowed to lecture on her own, but she still wasn't paid for her work. She left Europe and came to the United States in 1933, because of the rise of the Nazi regime and her Jewish background. Her body of work led to developments in geometry, algebra, and topology.
Math doesn't hold any prejudices or biasses, people are the ones who hold each other back. The subject of mathematics is open for discovery. While some genders have the stereotype of being stronger in some subjects, those stereotypes should not hold people back from doing what they excel at. Those such as Noether who went against stereotypes and continued working on what they loved, proved that the subject of math is ready for whatever you want to do with it, no matter the reaction it may evoke from others.
Monday, June 9, 2014
Weekly 5: Book Report/Review of The Joy of X
I chose to read the Joy of X by Steven Strogatz. The main reason I chose to read this book was because I actually know who Steven Strogatz is, and I had never heard of the other authors. I knew of him from his contributions to NPR's Radiolab. I would described Radiolab as a show geared toward educated people, who are looking to learn about something they are not already educated in. He is often called upon to contribute when the hosts are talking about a topic related to mathematics, and he does a great job of making the math understandable. Which is also why I thought his book would be an enjoyable read. Strogatz is also a professor of Applied Mathematics at Cornell University.
The Joy of X was split up into 30 very short chapters, which were divided between 6 different headings. The first section was Numbers. In the very first chapter Strogatz starts simply with an example from Sesame Street as to the value of numbers as a means of organization and simplification. He goes on in the chapters under the Numbers heading to cover the relationship between odds, evens, squares, and their visual representation via rock diagrams, negative multiplication, commutativity, division, and different numbering systems in history. The next section of chapters is titled Relationships. In the Relationship Chapters he dives into specific algebra problems and their solutions, i and imaginary numbers, and the all important quadratic formula. The third section was Shapes. In the shape chapters he works on breaking down the proof for the pythagorean theorem using squares on the edges of the triangle as we did earlier in our class. He also shows the proof for an equilateral triangle, discussed focusing and ellipses, the relationship between the conic sections, sin curves, and pi in relationship to a circle. The fourth section of the book is Change. In Change the different uses of calculus are discussed, as well as what the number e is and where it comes from, along with some fun differential equations that track Romeo and Juliet's love for one another. Of course math can be used to track fictional love. The fifth section was Data. Data dealt with the statistical arena of mathematics, with some interesting examples of doctors and lawyers who didn't know how to correctly interpret/solve statistical problem dealing with breast cancer, and the O.J. Simpson trail. Spoiler alert: Strogatz doesn't hid the fact he thinks Simpson was guilty. In the final section titled Frontiers, he wraps up with a look at Group Theory, great circles, a mobius strip he brought into his daughters classroom on career day, and problems with infinity. If I were to rename these sections with more direct names I would change Numbers to Arithmetic, Relationships to Algebra, Shapes to Geometry, Change to Calculus, Data to Statistic, and Frontiers to To Infinity and Beyond.
Strogratz attempts to cover math from one to infinity as the subtitle of the book states and I think he does a great job of it with the approximately 250 pages he uses. It is really quite the large task to attempt to essentially cover all of math in a way the average person would be able to follow. He keeps the chapters short and his explanations clear yet concise. His personal antic dotes kept it interesting and helped the reading move along fairly fast especially when I would otherwise have been getting a little bored reading some sections where I felt like he wasn't saying anything new to me, as a current math major. But there were also times in beginning of the book where I would say to myself "I've never thought about it that way". I would recommend this book to anyone interested in math, whether they have formal education in math, or they are just curious about the subject. His style of writing can make and depth of grasp on the subject make this book very readable and relatable to anyone interested in math. I wouldn't go as so far to say that someone who doesn't like math will enjoy this book. Strogatz isn't working miracles, but he would be able to clear some things up for those who did struggle with the subject before.
The Joy of X was split up into 30 very short chapters, which were divided between 6 different headings. The first section was Numbers. In the very first chapter Strogatz starts simply with an example from Sesame Street as to the value of numbers as a means of organization and simplification. He goes on in the chapters under the Numbers heading to cover the relationship between odds, evens, squares, and their visual representation via rock diagrams, negative multiplication, commutativity, division, and different numbering systems in history. The next section of chapters is titled Relationships. In the Relationship Chapters he dives into specific algebra problems and their solutions, i and imaginary numbers, and the all important quadratic formula. The third section was Shapes. In the shape chapters he works on breaking down the proof for the pythagorean theorem using squares on the edges of the triangle as we did earlier in our class. He also shows the proof for an equilateral triangle, discussed focusing and ellipses, the relationship between the conic sections, sin curves, and pi in relationship to a circle. The fourth section of the book is Change. In Change the different uses of calculus are discussed, as well as what the number e is and where it comes from, along with some fun differential equations that track Romeo and Juliet's love for one another. Of course math can be used to track fictional love. The fifth section was Data. Data dealt with the statistical arena of mathematics, with some interesting examples of doctors and lawyers who didn't know how to correctly interpret/solve statistical problem dealing with breast cancer, and the O.J. Simpson trail. Spoiler alert: Strogatz doesn't hid the fact he thinks Simpson was guilty. In the final section titled Frontiers, he wraps up with a look at Group Theory, great circles, a mobius strip he brought into his daughters classroom on career day, and problems with infinity. If I were to rename these sections with more direct names I would change Numbers to Arithmetic, Relationships to Algebra, Shapes to Geometry, Change to Calculus, Data to Statistic, and Frontiers to To Infinity and Beyond.
Strogratz attempts to cover math from one to infinity as the subtitle of the book states and I think he does a great job of it with the approximately 250 pages he uses. It is really quite the large task to attempt to essentially cover all of math in a way the average person would be able to follow. He keeps the chapters short and his explanations clear yet concise. His personal antic dotes kept it interesting and helped the reading move along fairly fast especially when I would otherwise have been getting a little bored reading some sections where I felt like he wasn't saying anything new to me, as a current math major. But there were also times in beginning of the book where I would say to myself "I've never thought about it that way". I would recommend this book to anyone interested in math, whether they have formal education in math, or they are just curious about the subject. His style of writing can make and depth of grasp on the subject make this book very readable and relatable to anyone interested in math. I wouldn't go as so far to say that someone who doesn't like math will enjoy this book. Strogatz isn't working miracles, but he would be able to clear some things up for those who did struggle with the subject before.
Thursday, June 5, 2014
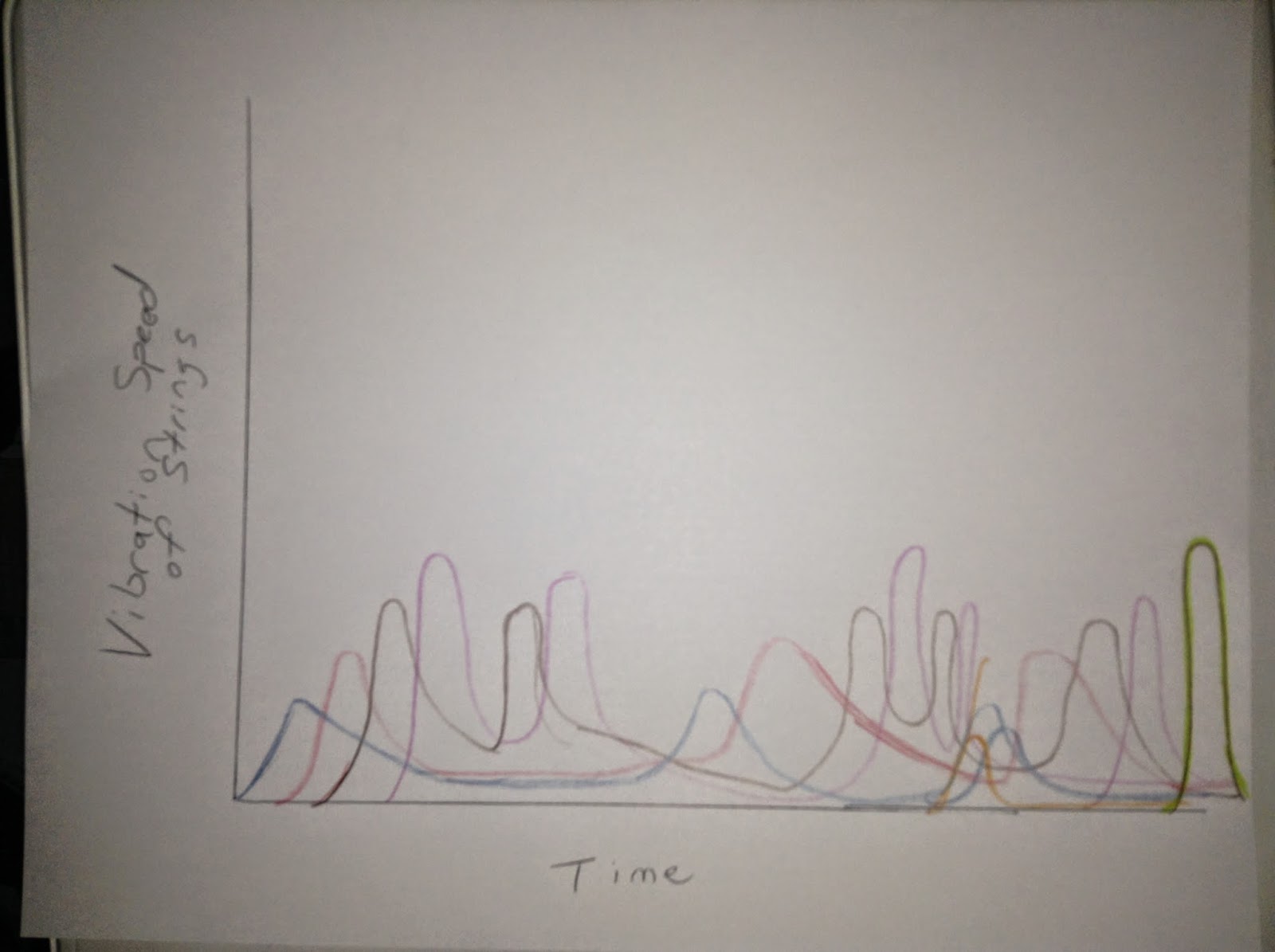
Daily 9: Graphing Vibration Speed
Weekly 4: Doing Math: Spirograh
For my forth weekly blog I decided to play around with the spirograph workbook on geogebratube. This workbook allows you to manipulate circle in many ways in order to trace the path of the circle or a connected circle to form certain unique designs.
My first design I made by tracing a single circle and moving it half the distance of the radius and tracing the circle again. I repeated the tracing 4 times in each of the three directions.
For my second design I allowed the program to roll and trace the paths of the arms attached to a circle moving around the outside of the original circle and another moving on the inside of the original circle. After the "loop" was completed I would change the color of the pen and shift the size of the arm to half it's previous size and complete another loop. I repeated this method multiple times, but used the same size original circle each time.
This last little design was made by tracing the path of the circle rolling around the inside of an original circle each color represents the path a circle that is half the size of the previous inner circle. The circle that was half the size of the original is the straight blue line. The path of the circle one quarter of the original is the green shape. The yellow figure is slightly smaller than one half of the circle used for the green shape, which is why the figures do not line up appropriately. I wasn't able to do 12.5 on the slider so I had to do 12 in order to make the yellow figure.
My first design I made by tracing a single circle and moving it half the distance of the radius and tracing the circle again. I repeated the tracing 4 times in each of the three directions.
This last little design was made by tracing the path of the circle rolling around the inside of an original circle each color represents the path a circle that is half the size of the previous inner circle. The circle that was half the size of the original is the straight blue line. The path of the circle one quarter of the original is the green shape. The yellow figure is slightly smaller than one half of the circle used for the green shape, which is why the figures do not line up appropriately. I wasn't able to do 12.5 on the slider so I had to do 12 in order to make the yellow figure.
Wednesday, May 28, 2014
Daily 7: Fibonacci Designs
For my Daily 7 I decided to play around with Fibonacci numbers in Geogebra. I made circles with radii of 1,1, 2,3,5,8,13, and 21, which are the first 7 Fibonacci numbers. I played around and rearranged them in some different shapes to try to make some Fibonacci art. Here are a few pictures of what I tried.
Weekly 3: Doing Math
For my third weekly work I thought I would expand on the Chinese Math handout. I worked on the story problems in that handout and thought I would come up with some of my own word problems that follow similar skills for solution. I will also post solutions to each problem.
1. A Corvette travels at a speed of 80 mph, a Malibu travels at a speed of 75 mph. If the Malibu leaves 1 hour before the Corvette, at what point will the Corvette catch up to the Malibu?
It will take the Corvette 15 hours from it's own start time to catch up with the Malibu. They will meet at 1200 miles.
2. Matt has 15 more stickers than Julie, and 3 more than Megan. Megan has 7 more stickers than Bob and Rachel combined. Rachel and Bob have the same amount of stickers. Rachel has 4 stickers. How many stickers does each person have?
Rachel has 4 stickers
Bob has 4 stickers
Megan has 15 stickers
Matt has 18 stickers
Julie has 3 stickers
3. A large pizza costs $12 and a medium pizza costs $9. A group of friends want to buy 3 large pizzas and 2 medium pizza and each wants to pay their fair share. There are 8 pieces per pizza and no person gets more than 5 slices and no person gets less than 3 slices. No one has change so they all pay to the nearest dollar and have two dollars extra. How many friends are paying for the pizzas? and how much did each friend pay?
There are 8 friends paying for pizza. The price of the pizza comes out to $54. Since there are two dollars extra we know that the friends money totaled $56. There are 40 pieces of pizza total and if no one get more than 5 pieces we know there are at least 8 friends. If no person gets less than 3 slices we know there can't be more than 13 friends. The only number that divides evenly into 56 between 8 and 13 is 8 so there has to be 8 friends paying for the pizza.
4. Let's do some more pizza math because pizza always sounds good to me. If two large pizzas a medium and a small cost $32, 1 large, 3 mediums, and 2 smalls cost $40, and 3 mediums and 2 larges cost $42, then how much does each size pizza cost?
A large pizza will cost about $10.36, a medium pizza will cost about $7.09, and a small pizza will cost about $4.18
This can be solved by using a system of equations such as:
2l+1m+2s=42, 1l+3m+2s=40, 2l+3m=42
I like to use matrices to solve systems of equations.
These are just a few examples of my own "story problems" that follow the same style as those given from the Nine Chapters.
1. A Corvette travels at a speed of 80 mph, a Malibu travels at a speed of 75 mph. If the Malibu leaves 1 hour before the Corvette, at what point will the Corvette catch up to the Malibu?
It will take the Corvette 15 hours from it's own start time to catch up with the Malibu. They will meet at 1200 miles.
2. Matt has 15 more stickers than Julie, and 3 more than Megan. Megan has 7 more stickers than Bob and Rachel combined. Rachel and Bob have the same amount of stickers. Rachel has 4 stickers. How many stickers does each person have?
Rachel has 4 stickers
Bob has 4 stickers
Megan has 15 stickers
Matt has 18 stickers
Julie has 3 stickers
3. A large pizza costs $12 and a medium pizza costs $9. A group of friends want to buy 3 large pizzas and 2 medium pizza and each wants to pay their fair share. There are 8 pieces per pizza and no person gets more than 5 slices and no person gets less than 3 slices. No one has change so they all pay to the nearest dollar and have two dollars extra. How many friends are paying for the pizzas? and how much did each friend pay?
There are 8 friends paying for pizza. The price of the pizza comes out to $54. Since there are two dollars extra we know that the friends money totaled $56. There are 40 pieces of pizza total and if no one get more than 5 pieces we know there are at least 8 friends. If no person gets less than 3 slices we know there can't be more than 13 friends. The only number that divides evenly into 56 between 8 and 13 is 8 so there has to be 8 friends paying for the pizza.
4. Let's do some more pizza math because pizza always sounds good to me. If two large pizzas a medium and a small cost $32, 1 large, 3 mediums, and 2 smalls cost $40, and 3 mediums and 2 larges cost $42, then how much does each size pizza cost?
A large pizza will cost about $10.36, a medium pizza will cost about $7.09, and a small pizza will cost about $4.18
This can be solved by using a system of equations such as:
2l+1m+2s=42, 1l+3m+2s=40, 2l+3m=42
I like to use matrices to solve systems of equations.
These are just a few examples of my own "story problems" that follow the same style as those given from the Nine Chapters.
Saturday, May 17, 2014
Weekly 2: Doing Math:Tesselation
Although it may not look like it. I spent about 2.5 hours constructing this "tessellation". I'm not the most gifted in the art department, but I took a stab at it. Two of my biggest problems with the construction were that I didn't have a protractor to make angles equal, and that I didn't start with an equilateral triangle in the center. Those two errors started to become more apparent as I started to branch out further with the design. Below is a picture on my tessellation spread across 9 sheets of 8.5 by 11 paper.
I started constructing this figure with just an equilateral triangle. As I mentioned I didn't have a protractor so I used the Pythagorean theorem to essentially make two right triangle back to back with a height which was twice the length of the base. From there I wanted to use different shapes to make a more unique construction. I used barn shaped hexagons which were hexagons with two 90 degree base angles. I simply filled in the rest of the space with whatever other shape would keep the general shape near a triangle. If I were to make this figure into a true tessellation I would make sure to use general shapes that would fill the rest of the figure into a larger equilateral triangle. By ensuring I have a larger equilateral triangle I would be able to surround it with three more copies of the figure, one on each side, and the pattern could repeat infinitely, by continuously adding copies to each new open side. If there is not a repeatable pattern present, then it is not a tessellation.
Thursday, May 15, 2014
Daily 3: Stomachion
After working on the paper version of the stomachion puzzle for about 2 hours and getting no where close to a solution I switched to the online geogebra version. I was able to finally find a solution with the geogebra version. A picture of the solution is below.
Monday, May 12, 2014
Nature of Mathematics: Axioms
According to Merriam-Webster an axiom is "a rule or principle that many people accept to be true." The origin of the word comes from the latin word axioma, which means worthy. In mathematics, axioms are statements which are accepted to be true without proof, because they seem to be evident. I guess you could say that axioms need no proof, because they are worthy. We do not question them, because we accept them and acknowledge them as true. One clear example of an axiom is the reflexive axiom used in algebra, which states "a number is equal to itself". This is easily accepted without argument or proof. I could show you that a=a, but by the definition of equality we know that a=a. If a was not equal to itself, then it would not be itself, and we would not be able to say anything for certain about a.
You could argue that axioms while not needing any proof themselves are the basic building blocks for mathematical proofs. In order to prove something, you must use axioms to support your work. Try to prove anything without using something that is already accepted to be true. You may think that a proof by example would be possible without using axioms. While you may be able to create some sort of proof without a formal axiom used, you will still rely on a universal truth to that is accepted to make your proof true. Let's say that I wanted to prove that 4-3=1. Maybe I would set out 4 apples on a table. Then I would take 3 of the apple away and eat them. This would leave one apple left over. I could claim that I did a proof by example without using any axioms. But would that really be true? The apples could reappear. That would contradict the proof, but we know that 3 apples will not magically appear from nowhere and present themselves on the table. Therefore, one rule that is accepted to be true without any proof is that objects do not spontaneously generate from no where. That statement could be viewed as an axiom in the apple proof.
Axioms are needed for creating and giving validity to proofs. They are also informally used in everyday life. People do not walk around astonished that aren't turning into dogs. We accept that we are humans and are not going to change into another animal. No one needs to prove to us that we are humans and are going to stay humans, we just accept this to be true. We further build proofs off of our accepted knowledge. This relates back to my previous blog about what is math. Axioms are not just used on paper, and neither is math. Math permeates into everyday life. If nothing is accepted to be true, then there is nothing that can be used to prove anything.
You could argue that axioms while not needing any proof themselves are the basic building blocks for mathematical proofs. In order to prove something, you must use axioms to support your work. Try to prove anything without using something that is already accepted to be true. You may think that a proof by example would be possible without using axioms. While you may be able to create some sort of proof without a formal axiom used, you will still rely on a universal truth to that is accepted to make your proof true. Let's say that I wanted to prove that 4-3=1. Maybe I would set out 4 apples on a table. Then I would take 3 of the apple away and eat them. This would leave one apple left over. I could claim that I did a proof by example without using any axioms. But would that really be true? The apples could reappear. That would contradict the proof, but we know that 3 apples will not magically appear from nowhere and present themselves on the table. Therefore, one rule that is accepted to be true without any proof is that objects do not spontaneously generate from no where. That statement could be viewed as an axiom in the apple proof.
Axioms are needed for creating and giving validity to proofs. They are also informally used in everyday life. People do not walk around astonished that aren't turning into dogs. We accept that we are humans and are not going to change into another animal. No one needs to prove to us that we are humans and are going to stay humans, we just accept this to be true. We further build proofs off of our accepted knowledge. This relates back to my previous blog about what is math. Axioms are not just used on paper, and neither is math. Math permeates into everyday life. If nothing is accepted to be true, then there is nothing that can be used to prove anything.
Thursday, May 8, 2014
What is Math?
I can not define what math is with a simple statement. But I will attempt to explain what I view math to be. It is numbers. It is variables. It is arithmetic. It is manipulation. It is also a way of interpreting information. When there is an issue or problem that needs to be solved; the sorting of information and weighing of options is math. The issue does not have to be how much water can fit in a fish tank to consist of a mathematical solution. Math is more than the basic manipulation of numbers, but a diverse way of thinking. Mathematical thinking is rational everyday thinking. I believe that mathematical logic often guides decision making. People are not robots without emotions, but when rational decisions must be made I believe the through process of organizing informations and comparing different options is the essence of mathematical thinking. I very much dislike writing formal proofs, but at the same time mathematical proofs are a great way to form logical arguments and confirm or deny possible truths. Mathematicians are not the only people who like to prove they are right. To me mathematical thinking is math. Pencil and paper and calculators and graphs do not need to be part of the picture for math to be present. Math permeates our lives, regardless of our feelings for it.
Top 4 Math Milestones in no particular order (drumroll please......)
1. Descartes' Coordinate Plane: His discovery/creation was a very beneficial representational tool to enhance understanding and development in algebra and geometry.
2. Riemann's Sum (Calculus): I believe that Riemann's Sum is the basic building block for understanding Calculus.
3. Pythagorean Theorem: Trianlges! I would venture a guess that the Pythagorean Theorem is the most well known mathematical theorem to the general public.
4. Invention of the Calculator: With the invention of the calculator and other math related technologies, new advancements were able to be developed with less time spent on simple arithmetic.
Subscribe to:
Posts (Atom)